Критерий хи-квадрат
Проведем мысленный эксперимент.
Мы скрестили два растения гороха. Получили следующее потомство:
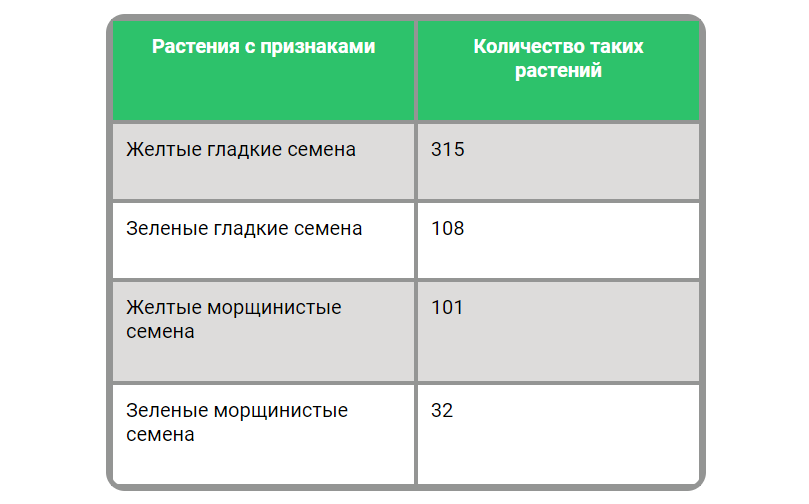
Что же делать с полученными результатами???
Так как мы с Вами исследователи, будем предлагать различные гипотезы. Я предлагаю такую:
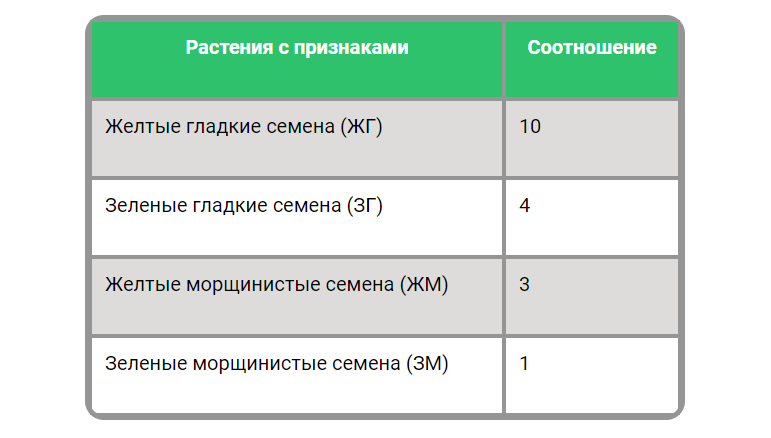
То есть я говорю, что мы получили в эксперименте расщепление 10 : 4 : 3 : 1.
Любой человек, который изучал генетику, скажет, что я говорю глупости, а в эксперименте наблюдается классическое расщепление 9 : 3 : 3 : 1.
Кто же прав?
Последователи Дарвина укрепляли позиции эволюционной теории в жарких спорах не без применения кулаков.
Мы с Вами живем, к сожалению не в 19 веке, сейчас в ученом сообществе для этих целей используют математику.
Инструментом для проверки гипотез расщепления служит хи-квадрат .
Как им пользоваться?
Хи-квадрат вычисляется по следующей формуле:
Т.е. сначала мы смотрим сколько у нас есть различных групп (растений/животных), чье соотношение мы проверяем. В нашем случае всего четыре группы: ЖГ, ЗГ, ЖМ и ЗМ. Затем мы выбираем гипотезу, которую хотим проверить. Выберем для начала мою: соотношение признаков 10 : 4 : 3 : 1.
В идеальном случае из 556 растений (315 + 108 + 101 + 32), которые получились в опыте, 10/18 (10/10+4+3+1) часть
имела бы желтые гладкие семена, 4/18 были бы с зелеными гладкими и т.д. В числах это 308,8 (556 * 10/18), 123,6 и т.д.
Такие гипотетические численные значения в формуле обозначены Ожидаемое . Соответственно Наблюдаемое - это то, что мы увидели в опыте: 315, 108 ... Вычислим значение хи-квадрат для гипотезы 10 : 4 : 3 : 1. хи-квадрат = (315 - 308,8) 2 /308,8 + (108 - 123,6) 2 /123,6 + (101 - 92,7) 2 /92,7 + (32 - 30,9) 2 /30,9 = 2,88
Теперь самое главное.
Что делать с вычисленным значением хи-квадрат?
Итак, что мы можем сказать о значении хи-квадрат, думая своей головой?
Чем оно больше, тем меньше наше доверие к гипотезе.
Потому что это означает, что наблюдаемые значения очень сильно отличаются
от ожидаемых.
Оценивать это значение можно только с учетом количества групп в опыте (в нашем случае их четыре).
Оценивают хи-квадрат обычно с помощью таблиц.
В таких таблицах пишут: по вертикали количество степеней свободы (для наших целей это число на единицу меньшее количества групп). Количество степеней свободы часто обозначают df (degree of freedom), а формула для его вычисления: df = кол-во групп - 1 по горизонтали: вероятность наблюдаемого значения быть случайным отклонением .
Сделаем умственное упражнение: если эта вероятность мала, то мы доверяем гипотезе или нет? Правильно! Нет.
Как определить количество групп?
Для этого не нужно быть изобретателем хи-квадрата. Достаточно уметь считать.
В нашем случае у нас раз, два, три, четыре! группы: (Желтые гладкие, Зеленые гладкие,
Желтые морщинистые, Зеленые морщинистые). Теперь вопрос на засыпку: если мы будем смотреть только наследование цвета, то сколько будет групп? Правильный ответ: 2 (желтые и зеленые).А чему будет равно кол-во степеней свободы?
Правильный ответ: 1 (количество групп минус 1).
Но вернемся к нашим баранам горохам.
Табл. 1. Значения хи-квадрат
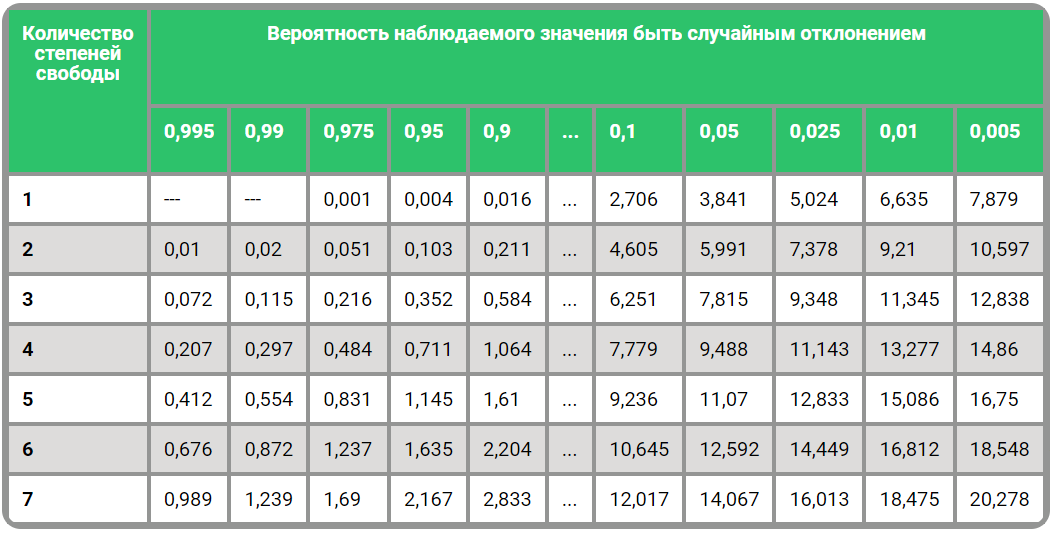
Попробуем оценить по этой таблице вероятность того, что отклонения от гипотезы 10 :4 : 3 : 1 в опыте случайны.
Количество степеней свободы: 3 . Значение хи-квадрат: 2,88 . Из табл. видно, что данная вероятность находится где-то между 0,9 и 0,1. Принято доверять гипотезе, если вероятность >= 0,1 (это называется уровень значимости 0,1), или если она >= 0,05 (уровень значимости 0,05).
Значит моя гипотеза вполне подходит, несмотря на то, что она мало согласуется с генетикой!
Попробуйте вычислить значение хи-квадрат для гипотезы 9 : 3 : 3 : 1 самостоятельно.
